This chapter is about finding the gradient of the tangent at a point on a graph. When you have completed it, you should be able to
1. calculate an approximation to the gradient at a point on a curve, given its equation
2. calculate the exact gradient at a point on a quadratic curve and certain other curves
3. find the equations of the tangent and normal to a curve at a point.
I'll just skip (1). So far in CIE exams, the examiners never asked the students to find approximation to the gradient. You don't need to prove the equations. However, you should know how to do (2) and (3).
You should know what normal and tangent to the curve are.
Some rules for differentiation
I assumed you already know the following rules :
If f(x) = ax2 + bx + c , then f ' (x) = 2ax + b.
If f(x) = x^n, where n is a positive interger/rational number, then f(x) = nx^n-1.
What is differentiation for?
.: 1. TO FIND THE GRADIENT OF THE CURVE :. so far until now this is the only reason to dy/dx the f(x). we will talk in details when you master this one.
Before i start off with the exam-type questions, i would like to show you how to differentiate these :
Questions :
Solutions :
Exams type questions :
let's say for second question, the new gradient, m would be -12.
Use this formula : - 1 / the gradient that is tangent to the graph, which is 1/12
To find the maximum and minimum of point of the graph, dy/dx the equation.
To find the nature of the graph, after you get the dy/dx value, dy/dx it again. You will then substitute in value of x , if the value of y > o, the point is minimum. If the value of y < 0, the point is maximum. You have to know this.
More exercises will be uploaded soon!
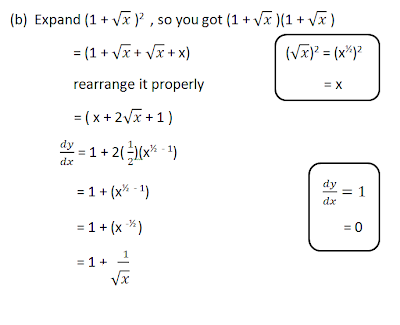
0 comments:
Post a Comment