An Arithmetic sequences, or arithmetic progression,is a sequence whose terms go up or down by constant steps.
The inductive definition for an arithmetic sequence has the form :
where the number d is called the common difference.
Eg 1: 1 3 5 7 9 ...
first term a = 1 and common difference d = 3.
Eg 2: 1 4 5 7 8 ...
This is not an arithmetic sequences. No solutions,
Example :
Senne would like to give a sum of money to a charity each year for 10 years. She decides to give $100 in the first year, and to increase her contribution by $20 each year. How much does she give in the last year, and how much does the charity receive from her altogether?
Although she makes 10 contributions, there are only 9 increases. So in last year she gives $(100 + 9x 200) = $280.
If the total amount the charity recievesis $S, then S = 100 + 120 + 140 + ... + 240 + 260 + 280.
With only 10 numbers it is easy enough to add these up, but you can also find the sum by a method similar to that used to find a formula for tn . If you add up the numbers in reverse order, you get
S = 280 + 260 + 240 + ... + 140 + 1200 + 100 .
Adding the two equations then gives
2S = 380 + 380 + 380 + ... + 380 + 380 + 380,
where the number 380 occurs 10 times. So
2S = 380 x 10 = 3800, giving S = 1900.
Over the 10 years the charity receives $1900.
The annual contributions
100,120,140, ...,240,260,280
form an arithmetic sequence, but if they are added as
100 + 120 + 140 + ... + 240 + 260 + 280.
They become an arithmetic series.
If the general arithmetic sequences
a , a + d , a + 2d , a + 3d , ...
has n terms in all, then from the first term to the last there are n - 1 steps of the common difference d. Denote the last term, un , by l. Then
l = a + (n - 1)d .
sum :
S = 1/2 n(a + l) = 1/2 n(2a + (n - 1)d)
Examples :
The sum of the first two terms of an arithmetic progression is 18 and the sum of the first four term is 52. Find the sum of the first eight terms.
S2 = 1/2 x 2 {2a + (2 - 1)(d) }
18 = 2a + d
S4 = 1/2 x 4 {2a + (4 - 1)(d) }
52 = 2(2a + 3d)
52 = 4a + 6d
Using simultaneous equation :
....
...
You will come out with the answer a = 7 , d = 4
S8 = 1/2 x 8 {2(7) + (8 - 1)(4) }
= 168 #


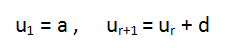
0 comments:
Post a Comment